Rotaciono kretanje krutog tela-Rotacija diska
Kruto telo – telo koje ima stalan oblik i zapreminu (prilikom kretanja ne menja ni oblik ni zapreminu).To je zapravo idealizovani koncept u mehanici koji predstavlja skup tačaka čije se međusobne udaljenosti tokom kretanja — tj. deformacija — ne menjaju. Drugim rečima, kad kažemo da je „telo kruto,“ podrazumevamo da je svaka dva proizvoljna njegova dela (tačke) razmaknuti fiksnom udaljenošću, bez obzira na sile koje deluju na telo. U realnosti sva materija malo elastično popušta, ali u okviru analize kretanja (naročito u klasičnoj mehanici) najčešće modeliramo predmete kao kruta tela kako bismo zanemarili deformacije.
Kruto telo može da se posmatra kao da je sastavljeno od velikog broja sitnih delova koji su obeleženi tačkama.
Kretanje krutog tela možemo posmatrati kao kombinaciju — ili posebne slučajeve — translacije i rotacije. U nastavku su najvažnije kategorije. Podela kretanja prema načinu kretanja pojedinih tačaka krutog tela:
-
translatorno
-
rotaciono
Translatorno kretanje
Translacija krutog tela
Translacija je kretanje kod kojeg se svaka tačka tela pomera uprav paralelno istoj putanji.
Paralelna translacija (često zovu „čista“ translacija): Svi delovi tela prate istu vektorsku pomerajnu.
Na primer, ako ceo predmet klizi pravo po stolu tako da se ne okreće, tada kažemo da telo vrši paralelnu translaciju.
Matematika: Ako je početna pozicija neke tačke r₀, a brzina tela je v (pomeranje konstantne brzine), onda je pozicija u trenutku t:
r(t) = r0 + v · tSvi pikseli/tačke se pomeraju jednako.


Rotaciono kretanje
Delići krutog tela se kreću po kružnim putanjama, a sve te kružnice leže u ravnima koje su međusobno paralelne
osa rotacije – prava kojoj pripadaju centri svih kružnica (može da prolazi kroz telo, a može biti i izvan tela)
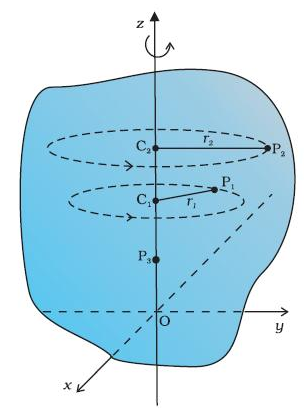
Fizičke veličine kojima se opisuje rotaciono kretanje
Ugaona brzina je fizička veličina kojom se opisuje brzina rotacije krutog tela.
Kada telo rotira njegove tačke nemaju iste brzine, jer tačke bliže osi su sporije, dok su tačke udaljenije od ose brže. Sve tačke tela pređu isti ugao za isto vreme tj. sve tačke tela imaju istu ugaonu brzinu. Zato se u rotaciji umesto brzine koristi ugaona brzina.
Ugaoni pomeraj
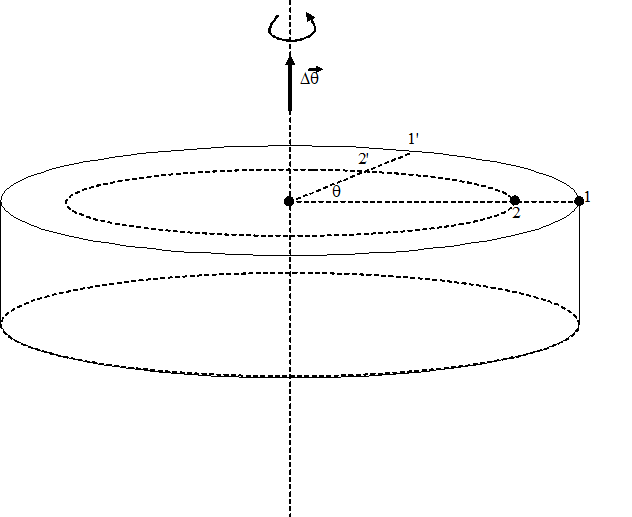
Tačke 1 i 2 se nalaze na različitim rastojanjima od ose rotacije. Za isto vreme prelaze različite puteve i imaju različite pomeraje.
Radijus vektori tačaka 1 i 2 za isto vreme opišu isti ugao (slika). Opisani ugao predstavlja fizičku veličinu kojom se opisuje rotaciono kretanje. Na osnovu opisanog ugla definiše se ugaoni pomeraj. Ugaoni pomeraj je vektorska veličina.
Ugaono ubrzanje

Rotacija diska
Pravac normalnog ubrzanja se poklapa sa poluprecnikom kružnice, a smer je uvek ka centru kružnice, pa se zato naziva i radijalno tj. centripetalno ubrzanje
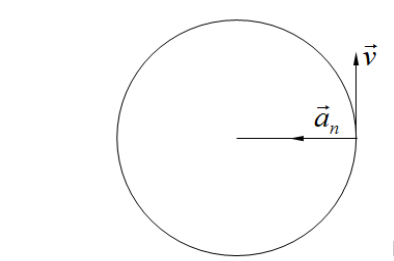
Rotacija diska
1. Cilj i zadatak simulacije
U ovoj lekciji ćemo kreirati interaktivnu simulaciju rotacije diska. Disk ima masu m i poluprečnik r.
Dva osnovna slučaja kretanja koje prikazaćemo su:
- Ravnomerno obrtanje – disk se okreće konstantnom ugaonom brzinom
ω. - Ravnomerno ubrzano obrtanje – disk počinje iz stanja mirovanja i ubrzava pod dejstvom konstantnog ugaonog
ubrzanja
α.
Koraci simulacije obuhvataju:
- Ažuriranje vremena:
t = t + Δt. - Ažuriranje ugaonog pomeraja:
Δφ = ω · Δt(za ravnomerno obrtanje) iliΔφ = ω·Δt + (α·Δt²)/2(za ravnomerno ubrzano obrtanje). - Ažuriranje ugla:
φ = φ + Δφ. - Izračunavanje položaja tačke
Mna obodu diska u dekartovim koordinatama:
x = r · cos(φ)
y = r · sin(φ)
Δt = 0.05 s dok se simulacija ne zaustavi.2. Ravnomerno obrtanje
Kada disk rotira ravnomerno, ugaona brzina ω je konstantna. U svakom koraku vremena Δt:
- Promena vremena:
t = t + Δt - Promena položaja:
Δφ = ω · Δt, pa je novi ugaoφ = φ + Δφ. - Koordinate tačke
Mna obodu diska:
x = r · cos(φ)
y = r · sin(φ)
U svakom trenutku crtam poziciju tačke M u 2D ravan (na DrawingPanel) i prikazujem 3D modeli diska koje možete rotirati kamerom.
Ovako učenik može vizuelno pratiti kako se svaka tačka diska kreće kružno istim ubrzanjem.
3. Ravnomerno ubrzano obrtanje
Sada hajde da uvedemo ugaono ubrzanje α. Disk počinje iz mirovanja (ili početne ugaone brzine ω0) i ubrzava.
Ugaono ubrzanje se definiše kao:
α = dω/dt [rad/s²]
Tokom istog vremenskog intervala Δt, ugaoni pomeraj Δφ raste jer se ugaona brzina menja:
Δφ = ω·Δt + (α·Δt²)/2ω trenutna ugaona brzina u datom koraku, a posle ovog koraka imače novu vrednost
ω = ω + α·Δt.
- Promena vremena:
t = t + Δt - Promena ugla:
φ = φ + ω·Δt + (α·Δt²)/2 - Ažuriranje ugaone brzine:
ω = ω + α·Δt - Koordinate tačke
M:x = r · cos(φ) y = r · sin(φ)
Ovde vidimo analogiju sa translatornim kretanjem:
s = s0 + v0·t + (a·t²)/2s sa φ, v0 sa ω i a sa α.
4. Moment sile i moment inercije
Da bi disk ubrzavao, mora da deluje spoljna sila. Međutim, na disk deluje raspodela sila, a ne samo jedna tačka. Bitan je moment sile
koja proizvodi tangencijalnu komponentu Ft. Za tačku M na rastojanju r od osi rotacije,
moment sile je:
M = Ft · r [N·m]
Normalna komponenta Fn prolazi kroz osu rotacije, pa njen moment iznosi nula. Dakle, samo tangencijalna komponenta doprinosi obrtanju.
Mera inertnosti kod kružnog kretanja je moment inercije I. Za disk je:
I = (m·r²)/2m masa diska, a r njegov poluprečnik.
Drugi Njutnov zakon za rotaciju glasi:
M = I · αTakođe, moment količine kretanja (rotacioni zamajac) diska oko fiksne ose je:
L = I · ωω predstavlja ugaonu brzinu diska.
5. Praktičan primer simulacije u EJS-u
U interaktivnom okruženju EJS, simulacija rotacije diska prikazuje sledeće komponente:
- 3D prikaz diska koji se kotrlja ili ubrzava oko vertikalne ose. Kamera se može rotirati kako bi se posmatralo kretanje iz različitih uglova.
-
2D „Top View“ (gornja projekcija) na
PlottingPanelgde se vidi kružna putanja tačkeMu ravni. -
Grafik ugaone brzine
ωu funkciji vremena na drugomPlottingPanel. -
Grafici kinetičke i potencijalne energije diska u odnosu na vreme na trećem
PlottingPanel, gde se jasno vidi prelaz energije od kinetičke do potencijalne i obrnuto kod ravnomerno ubrzanog kretanja.
Korisnik ima kontrolu nad parametrima:
- Poluprečnik
ri masamdiska. - Početna ugaona brzina
ω0ili ugaono ubrzanjeα. - Vremenski korak
Δtkojim se simulacija ažurira.
6. Zaključak
Rotacija diska je odličan primer za razumevanje dinamičkih zakona u rotacionom kretanju. Kroz simulaciju u EJS-u možete istražiti:
- Kako se ugaono ubrzanje menja kada se poveća ili smanji momenat sile
M. - Kako moment inercije
Idiska zavisi od mase i poluprečnika (I = m·r²/2). - Kako energija prelazi sa kutne (rotacione) na kinetičku (kod tačke na obodu) i nazad.
- Kako analogija sa translatornim kretanjem pomaže pri izračunavanju ugla
φi ugaone brzineωtokom vremena.
Proučavanje rotacije diska kroz interaktivnu simulaciju ne samo da čini učenje dinamičkih zakona zabavnim, već i omogućava duboko razumevanje kako sile i momenti utiču na realne objekte u svakodnevnom životu i inženjerskim primenama.