Simulacija kosog hica
Kosi hitac - uvod u simulaciju
Kosi hitac je kretanje koje se sastoji od kretanja nekog tela u ravni, brzinom V0 po pravcu koji zaklapa vektor brzine sa osom x.
Kosi hitac je složeno kretanje koje se može podeliti na dva nezavisna kretanja, vertikalno i horizontalno. Dok je komponenta horizontalnog kretanja ista sve vreme tokom kretanja, vertikalna komponenta se smanjauje za g*t zbog gravitacione sile koja vuće kuglu prema dole (slobodni pad). Na površini zemlje gravitociono ubrzanje iznosi približno g=9.81m/s² a
Primene kosog hica
Kosi hitac, osim što je udžbenički primer iz kinematike, ima mnoge zanimljive primene u svakodnevnom životu i sportu. Evo nekoliko primera koji ilustruju zašto je razumevanje putanje projektila izuzetno važno:
- Sportovi s loptom: Prilikom servisa u odbojci, lopta prati složenu paraboličnu putanju pre nego što pređe na protivničku stranu. Dobra postavka ugla i snage udarca omogućava lopti da preleti mrežu i padne tačno u zonu protivnika. Primer rešavanja zadatkaiz programiranja "Odbojka-servis" pročitajte na SvetProgramiranja: Odbojka – ispravan servis .
- Balistika i bezbednost: Pri projektovanju vatrenog oružja ili vatrogasnih creva, cilj je tačno predvideti gde će dinamisani mlaz vode ili zrna pogoditi, kako bi se obezbedila maksimalna efikasnost i bezbednost.
- Inženjering: Pri lansiranju vodenih fontana ili sistema za navodnjavanje, ugao izbacivanja vode određuje koliko daleko će mlaz dopreti do useva na poljima.
- Zabavni parkovi: Dizajn vodenih tobogana i tobogana na vodi koristi princip kosog hica kako bi gosti dobili uzbudljivu, ali bezbednu vožnju i sleteli na pravo mesto.
- 2D igrice: U mnogim jednostavnim igrama, kosi hitac predstavlja osnovu za kretanje likova i projektila. Na primer, bacanje granate, skok lika ili ispaljivanje strele prate paraboličnu putanju pod dejstvom gravitacije. Pogledajte kako se kosi hitac koristi prilikom kreiranja 2D igrice u Javi u ovom tutorijalu: Kreiranje 2D igrice u Java – simulacija kosog hica .
U svim ovim primerima, poznavanje osnovnih formula za horizontalno i vertikalno kretanje projektila omogućava precizno predviđanje putanje, optimizaciju ugla lansiranja i kontrolu dometa – bilo da želite poen u igri ili da navodnjavate useve pod savršenim zracima vode.
Sledeće formule opisuju kosi hitac:
Brzina u smeru x ose v u smeru osi x: v0X=v0*cos(α)
Brzina u smeru y ose v u smeru osi y: v0Y=v0*sin(α) - g*t
Pređeni put u smeru ose x: x=v0*t*cos(α)
Pređeni put u smeru ose y y=v0*t*sin(α) - g*t²/2
Vreme potrebno da telo postigne najvišu tačku putanje t=v0*sin(α)/g
Najveća postignuta visina HMax=v0²*(sin(α))²/(2*g)
Domet kosog hica D=v0²*sin(2*α)/g
Kosi hitac sa početne visine H0
Posmatrajmo sledeću simulaciju kosog hica prikazanoj na slici 1
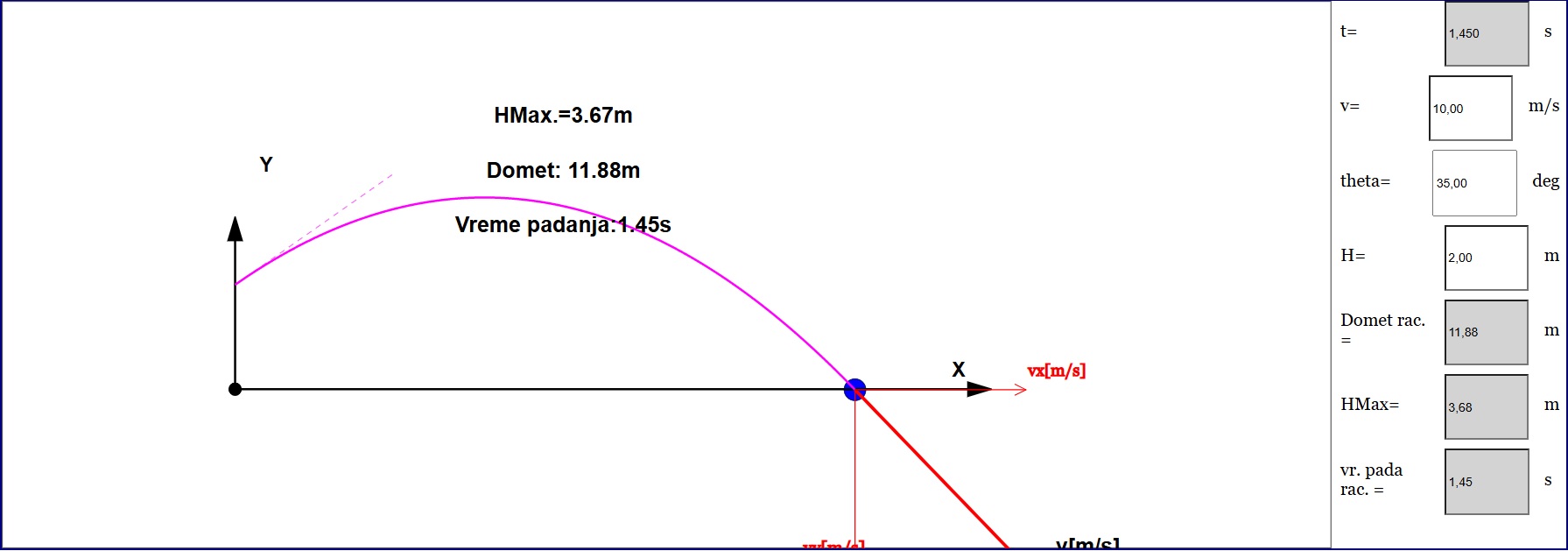
Na slici je prikazana kugla koja se nalazi na početnoj visini H0 od nivoa tla. Telo je bačeno i saopštena mu je neka početna brzina v0, čiji vektor ima pravac koji je pod uglom theta u odnosu na pozitivan smer X ose. Similacija je interaktivna i možete je isprobati na strani:
Određivanje dometa i maksimalne visine
1. Ukupno vreme leta (tD)
Horizontalni domet definisan je kao
D = v0x · tD
gde je v0x = v0 cos θ horizontalna komponenta početne brzine. Ukupno vreme leta tD može se izraziti kao:
tD = 2·tvD + tP
– tP je vreme penjanja od početne visine H0 do vrha oscilacije (i isto vreme spuštanja nazad na tu visinu),
– tP je vreme pada sa visine H0 na tlo.
2. Vreme penjanja i spuštanja do iste visine
Penjanje do vrha pod dejstvom gravitacije zadovoljava
0 = v0y – g·tP
⇒ t₁ = v0y / g
3. Vreme pada sa visine (H0)
Pad sa visine H0, pri kojem je brzina pri početku pada –v0y, rešava se iz kvadratne jednačine:
½·g·tP2 + v0y·tP – H0 = 0
Rešenje (pozitivni koren) je:
tP = (–v0y + √(v0y2 + 2·g·H0)) / g
4. Konačno vreme leta
Ubacivanjem u formulu za tD dobija se:
tD = 2·(v0y/g) + (–v0y + √(v0y2 + 2·g·H0)) / g
= (v0y + √(v0y2 + 2·g·H0)) / g
5. Domet
D = v0x · tD
6. Maksimalna visina (Hmax)
Visina penjanja (od H0 do vrha) data je formulom ravnomerno usporenog kretanja:
ΔH = v0y2 / (2·g)
Dakle, konačna maksimalna visina:
Hmax = H0 + v0y2 / (2·g)