Web Analytics
Klizanje tela niz strmu ravan
🇬🇧 English

Klizanje tela niz strmu ravan

Klizanje tela niz strmu ravan je klasičan problem iz dinamike u fizici. Kada telo klizi po ravni koja zaklapa ugao α sa horizontalom, komponenta gravitacione sile duž ravni je m·g·sin(α). Ako zanemarimo trenje, ubrzanje tela je:

a = g·sin(α)

U realnim uslovima često se uvodi koeficijent trenja μ, pa se rezultujuća sila duž ravni smanjuje za μ·m·g·cos(α), a ubrzanje postaje:

a = g·(sin(α) – μ·cos(α))

Simulacija u Processing‑u

Za interaktivnu simulaciju klizanja tela niz strmu ravan u Processing‑u, pogledajte primer: Primer strma ravan u Processing‑u .

Resursi

Teorija: Sile na nagnutoj ravni

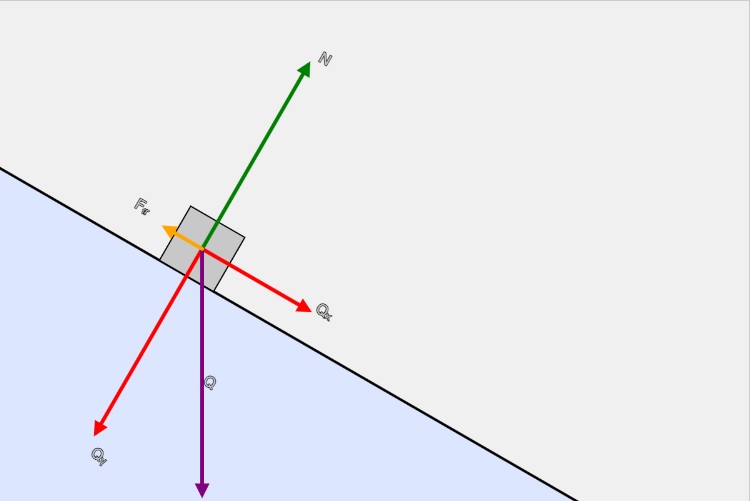
Na telo mase m koje leži na ravni nagnutoj pod uglom α deluju sledeće sile:

Telo na nagnutoj ravni sa silama

U simulaciji računamo akceleraciju duž ravni kao razliku paralelne komponente težine i trenja, podeljenu sa masom: 


a = (Qₓ – Fₜᵣ) / m 
  = [m·g·sin(α) – μ·m·g·cos(α)] / m
  = g·sin(α) – μ·g·cos(α)

Pozicija x(t) i brzina v(t) duž ravni dobijaju se standardnim kinematičkim izrazima: 


x(t) = x₀ + v₀·t + ½·a·t²
v(t) = v₀ + a·t

Ovako definisani izrazi ulaze u p5.js petlju draw(), gde se u svakoj iteraciji ažuriraju položaj i brzina tela po formuli iznad, a zatim se sve sile crtaju kao strelice u centru bloka.

Animacija klizanja tela niz strmu ravan pomoću alata p5.js

Ova animacija prikazuje kako blok klizi niz nagib pod uglom α koristeći JavaScript biblioteku p5.js. U centru bloka crtaju se sile: Qₓ (paralelna komponenta težine), Qᵧ (normalna komponenta), N (normalna sila) i Fₜᵣ (trenje).

U svakoj iteraciji izračunavamo ubrzanje a = g·sin(α) – μ·g·cos(α), ažuriramo brzinu i položaj bloka, i crtamo strelice koje predstavljaju sve sile. Kada blok stigne do kraja ravni, animacija se kratko zaustavlja, blok se vraća u početni položaj i proces se ponavlja.

Primer animacije:

U nastavku možete dodati kontrole za ugao nagiba, koeficijent trenja ili početnu brzinu bloka, kako biste eksperimentisali sa ponašanjem simulacije.

Ova simulacija prikazuje klizanje tela niz strmu ravan i koristi biblioteku p5.js. Prikazani su i vektori sila koji deluju na telo: težina (Q), njene komponente (Qₓ i Qᵧ), normalna sila (N) i sila trenja (Fₜᵣ).

Parametri simulacije su definisani kao globalne promenljive: ugao nagiba, početna pozicija bloka, veličina bloka, gravitaciono ubrzanje i koeficijent trenja. U setup() funkciji kreira se canvas i smešta se u div sa ID-jem sketch-holder.

Koordinatni sistem je rotiran tako da x osa prati nagib, što omogućava jednostavnije izračunavanje položaja tela i komponenti sila. Funkcije translate(), rotate(), push() i pop() koriste se za lokalnu transformaciju sistema i vraćanje na prethodno stanje nakon crtanja pojedinačnih elemenata.

Struktura koda je podeljena u više funkcija:

index.html

<!DOCTYPE html>
<html>
<head>
  <meta charset="utf-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">

  <!-- Učitavanje biblioteka -->
  <script language="javascript" type="text/javascript" src="libraries/p5.min.js"></script>
  <script language="javascript" type="text/javascript" src="StrmaRavanOsnovnaSaVektorima.js"></script>

  <style>
  body { margin: 0; padding: 0; }
  #sketch-holder {
    width: 100%;
    max-width: 600px;
    margin: 20px auto;
    border: 1px solid #ccc;
  }
  </style>
</head>

<body>
  <div id="sketch-holder"></div>
</body>
</html>

StrmaRavanOsnovnaSaVektorima.js

// Simulacija klizanja niz strmu ravan

// Definisanje fizičkih i geometrijskih parametara
let alpha; // Ugao nagiba ravni
const blockSize = 50; // Veličina bloka (kvadrata)
const g = 9.81; // Gravitaciono ubrzanje
const mu = 0.2; // Koeficijent trenja

// Veličine za praćenje kretanja
let a; // Ubrzanje
let v = 0; // Brzina
let s = 0; // Pređeni put
const dt = 1/60; // Vremenski korak (60 FPS)

// Početne pozicije i granice
const startX = 150; // Početna x koordinata bloka
let inclineY; // Vertikalna pozicija nagiba
let maxS; // Maksimalno rastojanje koje blok može preći

// Promenljive za kontrolu stanja simulacije
let state = 'running'; // Trenutno stanje ('running' ili 'pause')
let pauseStart = 0; // Vreme početka pauze
const pauseDuration = 1000; // Trajanje pauze u milisekundama

function setup() {
  // Inicijalizacija platna i podešavanja
  const canvas = createCanvas(600, 400);
  canvas.parent('sketch-holder');

  alpha = PI / 6; // 30 stepeni
  inclineY = height / 3;
  maxS = width - startX;

  a = g * sin(alpha) - mu * g * cos(alpha); // Ubrzanje niz nagib

  // Podešavanja za crtanje
  angleMode(RADIANS);
  rectMode(CENTER);
  textAlign(LEFT, CENTER);
}

function draw() {
  background(240); // Osvežavanje pozadine
  drawIncline(); // Crtanje strme ravni
  updateMotion(); // Ažuriranje pozicije bloka
  drawBlockAndForces(); // Crtanje bloka i sila
}

function updateMotion() {
  if (state === 'running') {
    v += a * dt; // Povećanje brzine
    s += v * dt; // Povećanje pređenog puta

    if (s >= maxS) {
      s = maxS; // Zaustavi kretanje kada stigne do kraja
      state = 'pause';
      pauseStart = millis();
    }
  } else if (state === 'pause') {
    if (millis() - pauseStart >= pauseDuration) {
      s = 0;
      v = 0;
      state = 'running'; // Resetuj simulaciju
    }
  }
}

function drawIncline() {
  push();
  translate(0, inclineY); // Pomeri poreklo
  rotate(alpha); // Rotiraj celu ravan

  // Crtanje trougla koji predstavlja nagnutu ravan
  noStroke();
  fill(220, 230, 255);
  triangle(0, 0, width*1.5, 0, 0, height);

  // Linija po kojoj se kliza blok
  stroke(0);
  strokeWeight(2);
  line(0, 0, width*1.5, 0);
  pop();
}

function drawBlockAndForces() {
  // Računanje komponenti sila
  const Qx = g * sin(alpha),
        Qy = g * cos(alpha),
        N  = Qy,
        Ftr= mu * N,
        scaleF = 20; // Faktor skaliranja za prikaz vektora

  // Izračunavanje pozicije bloka
  let bx = startX + s,
      by = inclineY + bx * tan(alpha);

  push();
  translate(bx, by);
  rotate(alpha);
  translate(0, -blockSize/2);

  // Crtanje bloka
  fill(200);
  stroke(0);
  rect(0, 0, blockSize, blockSize);

  // Crtanje vektora sila i oznaka
  drawArrow(createVector(0,0), createVector(Qx*scaleF, 0), 'red');
  text('Qₓ', Qx*scaleF+5, -5);

  drawArrow(createVector(0,0), createVector(0,Qy*scaleF), 'red');
  text('Qᵧ', 5, Qy*scaleF+15);

  drawArrow(createVector(0,0), createVector(Qx*scaleF,Qy*scaleF), 'purple');
  text('Q', Qx*scaleF/2+5, Qy*scaleF/2+5);

  drawArrow(createVector(0,0), createVector(0, -N*scaleF), 'green');
  text('N', 5, -N*scaleF-10);

  drawArrow(createVector(0,0), createVector(-Ftr*scaleF, 0), 'orange');
  text('Fₜᵣ', -Ftr*scaleF-30, -5);
  pop();
}

Objašnjenje koda animacije klizanja

Ovako definisani koraci čine kod modularnim, lakšim za razumevanje i održavanje. Za detaljnije objašnjenje transformacija, pogledajte dokumentaciju p5.js za push()/pop(), translate() i rotate().

© Copyright 2019 Slobodan Tršek