Sliding on an Inclined Plane

Sliding on an inclined plane is a classic dynamics problem in physics. When a block slides down a plane tilted at angle α to the horizontal, the component of the gravitational force along the plane is m·g·sin(α). Neglecting friction, the block’s acceleration is:

a = g·sin(α)

In real situations, we often introduce a friction coefficient μ, reducing the net force along the plane by μ·m·g·cos(α), so the acceleration becomes:

a = g·(sin(α) – μ·cos(α))

Processing Simulation

For an interactive Processing simulation of sliding on an inclined plane, see: Example of inclined plane in Processing .

Resources

Theory: Forces on an Inclined Plane

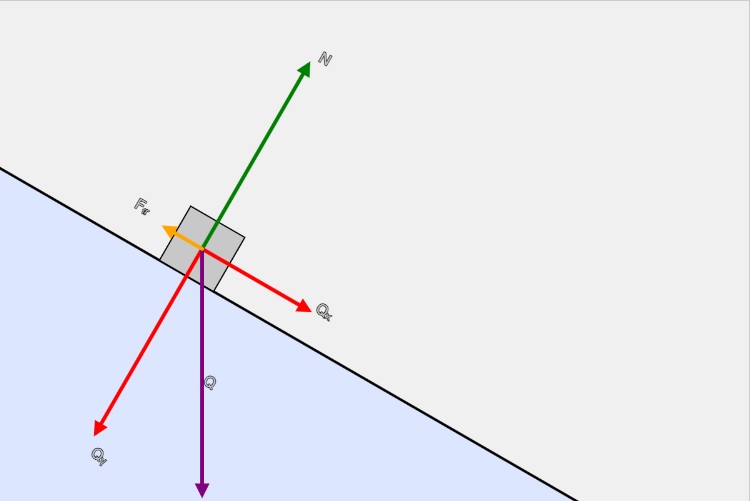
A block of mass m on a plane inclined at angle α is subject to:

Weight Q = m·g, directed vertically downward.
Component of weight parallel to plane Qₓ = Q·sin(α) = m·g·sin(α), directed down the slope.
Component of weight normal to plane Qᵧ = Q·cos(α) = m·g·cos(α), directed into the plane.
Normal force N = Qᵧ = m·g·cos(α), opposing Qᵧ.
Friction Fₜᵣ = μ·N = μ·m·g·cos(α), opposing motion down the plane.

Block on an inclined plane with forces

In the simulation we compute the acceleration along the plane as the net force divided by mass:


a = (Qₓ – Fₜᵣ) / m 
  = [m·g·sin(α) – μ·m·g·cos(α)] / m
  = g·sin(α) – μ·g·cos(α)

The position x(t) and velocity v(t) along the plane follow standard kinematic formulas:


x(t) = x₀ + v₀·t + ½·a·t²
v(t) = v₀ + a·t

These expressions drive the p5.js draw() loop, updating the block’s position and velocity each frame and drawing all force vectors.

Inclined Plane Simulation with p5.js

This animation shows a block sliding down a slope at angle α using the JavaScript p5.js library. Force vectors are drawn at the block’s center: Qₓ (parallel weight), Qᵧ (normal weight), N (normal force) and Fₜᵣ (friction).

Each frame we compute acceleration a = g·sin(α) – μ·g·cos(α), update velocity and position, and draw arrows representing each force. When the block reaches the end of the incline, the animation pauses briefly, resets the block to the start, and repeats.

Animation Example:

You can add controls for the incline angle, friction coefficient, or initial block speed to experiment with the simulation’s behavior.

This simulation uses the p5.js library to model sliding on an inclined plane. The force vectors shown are: weight (Q), its components (Qₓ, Qᵧ), normal force (N) and friction (Fₜᵣ).

Simulation parameters are defined as global variables: incline angle, block start position, block size, gravitational acceleration, and friction coefficient. In setup(), the canvas is created and placed into the div with ID sketch-holder.

The coordinate system is rotated so the x-axis aligns with the slope, simplifying position and force computations. The translate(), rotate(), push() and pop() functions handle local transformations and reset the drawing state.

Code structure is modularized into several functions:

drawIncline() — draws the inclined plane
drawBlockAndForces() — draws the block and force vectors
updateMotion() — updates block motion with friction
drawArrow() — helper for drawing arrows

index.html

<!DOCTYPE html>
<html>
<head>
  <meta charset="utf-8">
  <meta name="viewport" content="width=device-width, initial-scale=1.0">

  <!-- Učitavanje biblioteka -->
  <script language="javascript" type="text/javascript" src="libraries/p5.min.js"></script>
  <script language="javascript" type="text/javascript" src="StrmaRavanOsnovnaSaVektorima.js"></script>

  <style>
  body { margin: 0; padding: 0; }
  #sketch-holder {
    width: 100%;
    max-width: 600px;
    margin: 20px auto;
    border: 1px solid #ccc;
  }
  </style>
</head>

<body>
  <div id="sketch-holder"></div>
</body>
</html>

StrmaRavanOsnovnaSaVektorima.js

// Simulation of sliding down an inclined plane

// Define physical and geometric parameters
let alpha; // Angle of incline
const blockSize = 50; // Size of the block (square)
const g = 9.81; // Gravitational acceleration
const mu = 0.2; // Coefficient of friction

// Variables for tracking motion
let a; // Acceleration
let v = 0; // Velocity
let s = 0; // Distance traveled
const dt = 1/60; // Time step (60 FPS)

// Initial positions and limits
const startX = 150; // Initial x-coordinate of the block
let inclineY; // Vertical position of the incline
let maxS; // Maximum distance the block can travel

// Variables for simulation state control
let state = 'running'; // Current state ('running' or 'pause')
let pauseStart = 0; // Start time of pause
const pauseDuration = 1000; // Pause duration in milliseconds

function setup() {
  // Initialize canvas and settings
  const canvas = createCanvas(600, 400);
  canvas.parent('sketch-holder');

  alpha = PI / 6; // 30 degrees
  inclineY = height / 3;
  maxS = width - startX;

  a = g * sin(alpha) - mu * g * cos(alpha); // Acceleration along the incline

  // Drawing settings
  angleMode(RADIANS);
  rectMode(CENTER);
  textAlign(LEFT, CENTER);
}

function draw() {
  background(240); // Refresh background
  drawIncline(); // Draw incline
  updateMotion(); // Update block position
  drawBlockAndForces(); // Draw block and forces
}

function updateMotion() {
  if (state === 'running') {
    v += a * dt; // Increase velocity
    s += v * dt; // Increase traveled distance

    if (s >= maxS) {
      s = maxS; // Stop movement when reaching the end
      state = 'pause';
      pauseStart = millis();
    }
  } else if (state === 'pause') {
    if (millis() - pauseStart >= pauseDuration) {
      s = 0;
      v = 0;
      state = 'running'; // Reset simulation
    }
  }
}

function drawIncline() {
  push();
  translate(0, inclineY); // Translate origin
  rotate(alpha); // Rotate entire incline

  // Draw triangle representing the incline
  noStroke();
  fill(220, 230, 255);
  triangle(0, 0, width*1.5, 0, 0, height);

  // Line along which the block slides
  stroke(0);
  strokeWeight(2);
  line(0, 0, width*1.5, 0);
  pop();
}

function drawBlockAndForces() {
  // Calculate force components
  const Qx = g * sin(alpha),
        Qy = g * cos(alpha),
        N  = Qy,
        Ftr= mu * N,
        scaleF = 20; // Scaling factor for force vectors

  // Calculate block position
  let bx = startX + s,
      by = inclineY + bx * tan(alpha);

  push();
  translate(bx, by);
  rotate(alpha);
  translate(0, -blockSize/2);

  // Draw block
  fill(200);
  stroke(0);
  rect(0, 0, blockSize, blockSize);

  // Draw force vectors and labels
  drawArrow(createVector(0,0), createVector(Qx*scaleF, 0), 'red');
  text('Qₓ', Qx*scaleF+5, -5);

  drawArrow(createVector(0,0), createVector(0,Qy*scaleF), 'red');
  text('Qᵧ', 5, Qy*scaleF+15);

  drawArrow(createVector(0,0), createVector(Qx*scaleF,Qy*scaleF), 'purple');
  text('Q', Qx*scaleF/2+5, Qy*scaleF/2+5);

  drawArrow(createVector(0,0), createVector(0, -N*scaleF), 'green');
  text('N', 5, -N*scaleF-10);

  drawArrow(createVector(0,0), createVector(-Ftr*scaleF, 0), 'orange');
  text('Fₜᵣ', -Ftr*scaleF-30, -5);
  pop();
}

Explanation of the Sliding Animation Code

Global variables: incline angle alpha (positive means the plane slopes down from left to right), center position of the block blockPos, block size blockSize, gravitational acceleration g, friction coefficient mu.
In the setup() method:
1. Create the canvas with createCanvas(600, 400) and attach it to the <div id="sketch-holder"> using canvas.parent(...).
2. Set alpha = PI/6 and calculate the starting position:
```
startX = 150;
startY = startX * tan(alpha);
blockPos = createVector(startX, startY);
```
3. Configure drawing modes with angleMode(RADIANS), rectMode(CENTER), and textAlign(LEFT, CENTER).
In the draw() method:
1. Set background color: background(240).
2. Call drawIncline() (to draw the line and filled triangle) and drawBlockAndForces() (to draw the block and force vectors).
3. Call updateMotion() to update velocity and position, handle pause, and reset.
The drawing routines use:
- push() / pop() — save and restore the transformation matrix.
- translate(x, y) — move the coordinate system.
- rotate(α) — rotate the coordinate system.
… (the ellipsis indicates that you can apply multiple translate/rotate calls between push() and pop(), and all transformations will be undone after pop()).

The updateMotion() function (or inline code in draw()) works as follows:

// acceleration along the incline
blockAcc = g * sin(alpha) - mu * g * cos(alpha);
// each frame:
blockVel += blockAcc * deltaT;
blockPos.x += blockVel * deltaT;
// check if the block reached the end, then pause/reset…

These steps make the code modular, easier to understand and maintain. For more details on transformations, see the p5.js documentation for push()/pop(), translate(), and rotate().