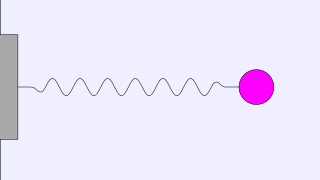
Mass–Spring System on a Horizontal Surface

We consider a system where a ball of mass m is attached to one end of a spring with stiffness constant k, while the other end of the spring is fixed to a rigid surface. The system rests on a frictionless horizontal surface, allowing the ball to move freely along the spring's axis.

When an external force F is applied to the ball and stretches the spring by a distance x from the equilibrium position, the spring responds with a restoring force according to Hooke’s law:
Fs = −k·x
Here, the minus sign indicates that the force is directed opposite to the displacement, pulling the system back toward equilibrium.

When the force F stops acting, there is no longer any external cause for movement, but the restoring force of the spring pushes the ball back toward the center. Due to inertia, the ball overshoots the equilibrium position and continues to the opposite side, where it is again slowed down and pulled back. This cycle repeats – the ball oscillates around the equilibrium point.

The equation of motion is given by the differential equation:
m·d²x/dt² + k·x = 0
This is the classical form of a linear harmonic oscillator. The solution is:
x(t) = A·cos(ω·t + φ),
where ω = √(k/m) is the angular frequency, A the amplitude of oscillation, and φ the phase shift.

In a harmonic oscillator, energy is continuously exchanged between the spring’s potential energy U = ½·k·x² and the ball’s kinetic energy K = ½·m·v², while the total energy remains constant.

Animation Example:

Below you can adjust the values of mass m, spring stiffness k, and initial stretch A to see how the frequency and shape of oscillations change in real time.