TRANSLATION OF A RIGID BODY
Rigid body translation is the motion in which all points of the body move at all times in a plane that remains parallel to a fixed reference plane.
Translation consists of a combination of the two simplest types of motion:
- translation
-
rotation about an axis whose direction is fixed but whose position in space changes over time.
During rigid body motion, all its parts move in the same way and follow identical paths.
Examples of Rigid Body Translation
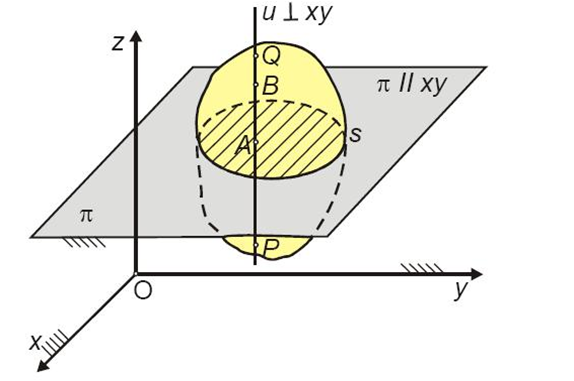
We observe the positions of the cross-section S at times t0, t1 and t2
(noting the material segment and its positions):
Rigid body translation consists of two fundamental motions: translation
and rotation about an axis passing through a chosen point in the plane of figure S, perpendicular to that plane.
Moving the representative cross-section from one position to another can be achieved
-
by one translation (of the section together with point C) plus one rotation
about point C by an angle φ
or
-
by a single rotation about the same axis of rotation.
The final equations of rigid body translation (laws of translation) are:
xC = xC(t), yC = yC(t), φC = φC(t).
The first two equations refer to the translation of the wheel in the xOy plane, while
the third refers to its rotation about the center by angle φ.
Rigid Body Translation with Constant Angular Velocity ω
Equations of translation for a point during a time step of Δt seconds:
Instantaneous Center of Rotation
Rigid body translation can be viewed as a pure rotation around the instantaneous rotation axis.
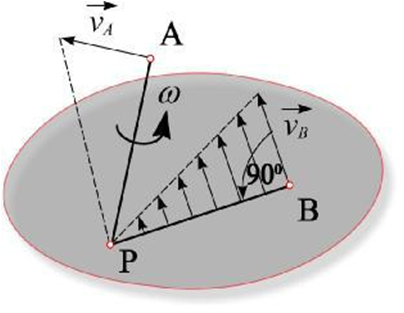
In the plane of cross-section, there is always a point where the velocity is zero.
This is the intersection point of the instantaneous rotation axis with the plane, called the instantaneous center of velocity P.
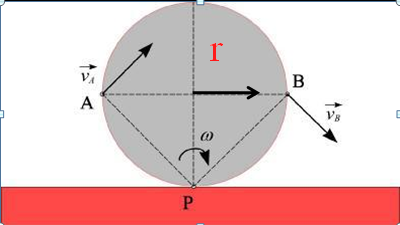
Rolling Without Slipping of a Cylinder on a Fixed Surface
Since there is no slipping at the contact point between the cylinder and the surface,
the velocity of that point on the cylinder is zero. Therefore, this point is the instantaneous center of velocity.
The velocities of arbitrary points A and B are:
vA = ω × AP
vB = ω × BP
vC = ω · r
Acceleration in Rigid Body Translation
In translation, the acceleration of any point A equals the vector sum of the acceleration of C
and the acceleration of A about C.
Rigid Body Translation with Angular Acceleration a – Dynamics
Similar to the disk rotation case, if we add the translational motion of the center: