Disc Rotation: Task 1 Solution

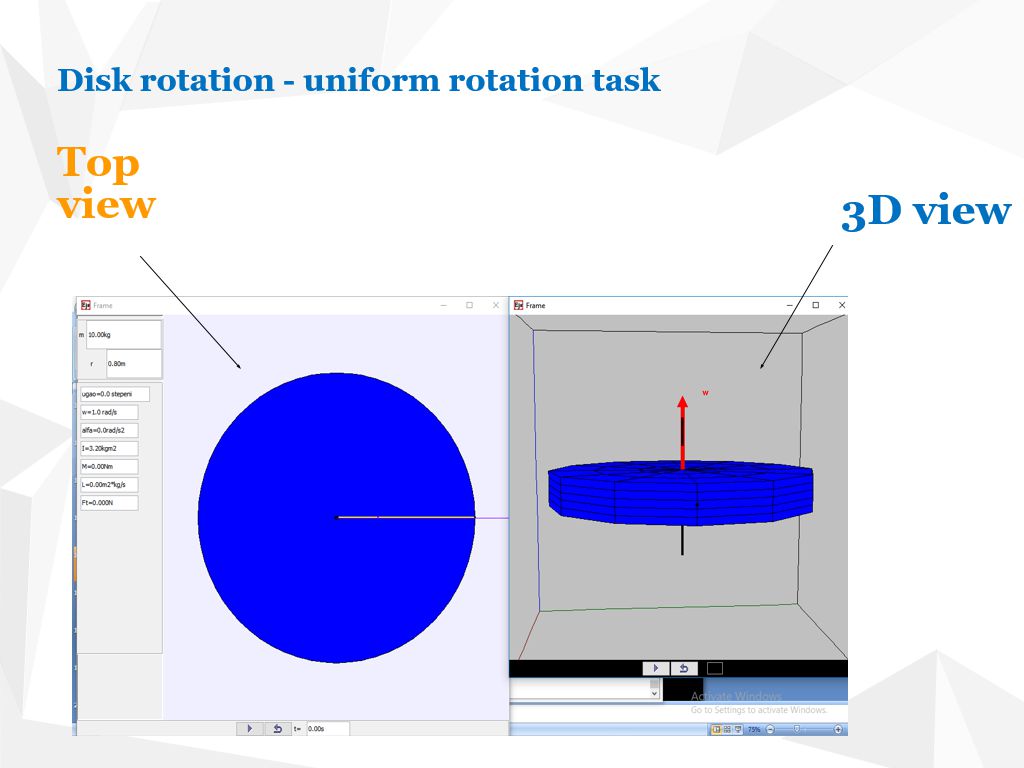
We present a two-view simulation (2D “top” view and 3D perspective) of a uniformly rotating disc. Each step shows how we track a point on the rim and convert between polar and Cartesian coordinates.

2D Top View and 3D Perspective

The simulation renders both a bird’s-eye view (showing the disc’s outline and rotation) and a 3D view (providing depth).

Side-by-side 2D top view and 3D perspective of a uniformly rotating disc
Figure 1. 2D top view and 3D perspective of the rotating disc.

Marking a Fixed Point and Its Velocity Vector

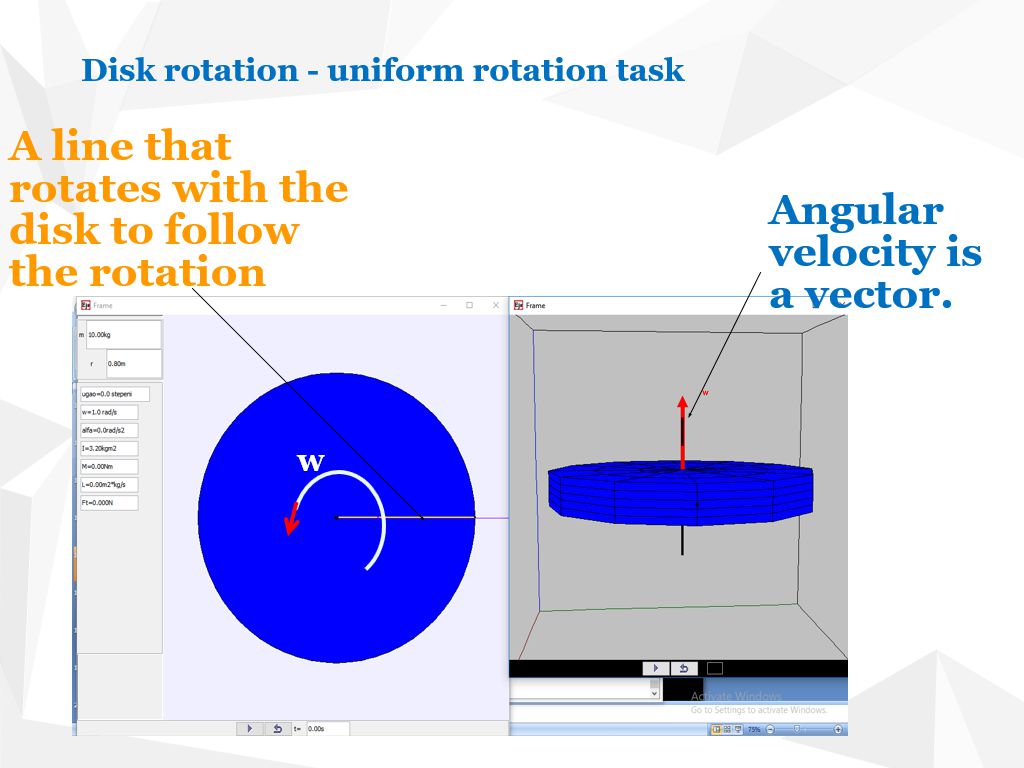
We attach a radial line to point M on the rim. Its instantaneous velocity vector ω·r is shown tangentially.

Disc with a radial marker and its tangential velocity vector
Figure 2. A radial line to point M and its tangential velocity arrow.

Angular Displacement Over Small Time Steps

Let time advance in uniform increments dt (e.g. 0.05 s). The angular displacement per step is dφ = ω·dt.

Illustration of a fixed point M on the disc and the small angular step dφ
Figure 3. Point M on the rim and its angular step dφ.

Iterative Update Rules

At each iteration:

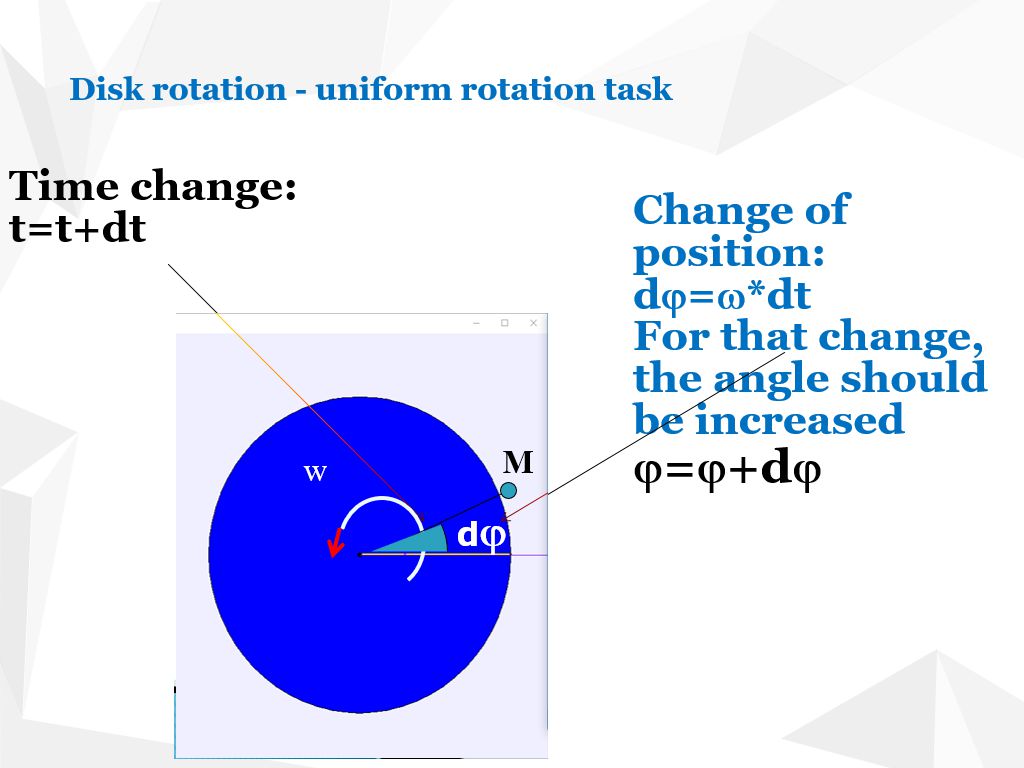
Flowchart showing update of time and angle in the simulation loop
Figure 4. Updating time and angle at each simulation step.

From Polar to Cartesian Coordinates

To plot point M in the canvas, convert its polar coordinates (r,φ) into:

x = r·cos(φ)    y = r·sin(φ)

Diagram showing conversion from polar (r, φ) to Cartesian (x, y)
Figure 5. Converting polar coordinates (r,φ) into (x,y).